투시도법 _ 3점 투시도법 / 3 point perspective
저서 '드로잉의 시작과 끝'에서 못 다한 이야기
대부분 사람들 특히 미술을 전공한 사람들도 3점 투시도법에선 소실점(Vanishing Point )이
3개라고 암기하고 있습니다. 그 증거로 내가 '드로잉의 시작과 끝'이란 책을 출간하기 바로 전에
원고 내용을 미술을 전공한 20명 내외의 선생님들께 감리를 부탁했었습니다.
그런데 생각지도 않았던 이 3점 투시도법 이론에 대부분 선생님들과 출판사 측에서
3점 투시도법의 내용을 바꿔야 한다는 말이 나왔습니다. 그 후로 난 일주일 쯤 고민하다가
이론적으로 내가 틀리지 않음을 증명할 내용을 첨부하기에 이르게 되었습니다.
이 글을 읽으시는 분들이나 책을 구입해서 보신 분들이 충분히 이해가 가도록
이곳을 통해서 설명하고자 합니다. 이 게시 글과 다음에 게시 할 내용을 잘 읽어주시길 바랍니다.
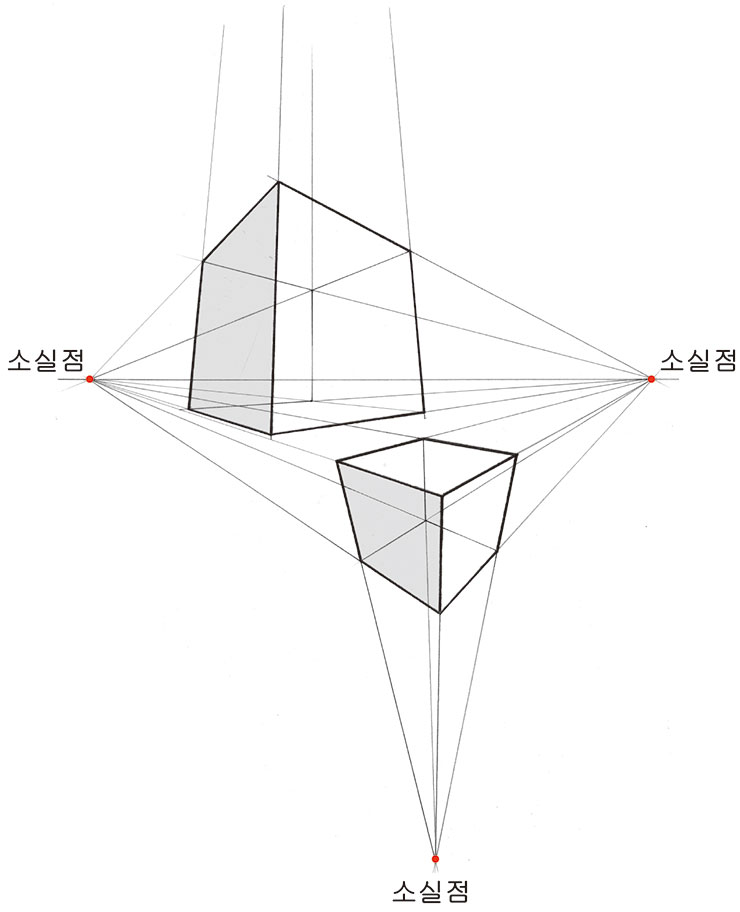
3점 투시도법의 가장 중요한 포인트는 'z'축 입니다. 1점 투시도법 바로 전 게시 글
설명한 'X'축, 'Y'축, 'Z'축 기억하시죠. 1, 2점 투시도법은 같은 투시도법이고
3점 투시도법만이 다른 투시도법 입니다. 1, 2점 투시도법은 'Z'축이 항상 수직이며,
3점 투시도법만이 'Z'축에 변화가 생깁니다. 그래서 3점 투시도법에서
소실점은 2개 이거나 3개 일 수 있습니다. 일단 소실점이 3개인 3점 투시도법의
아래 이미지를 잘 봐 주시길 바랍니다.
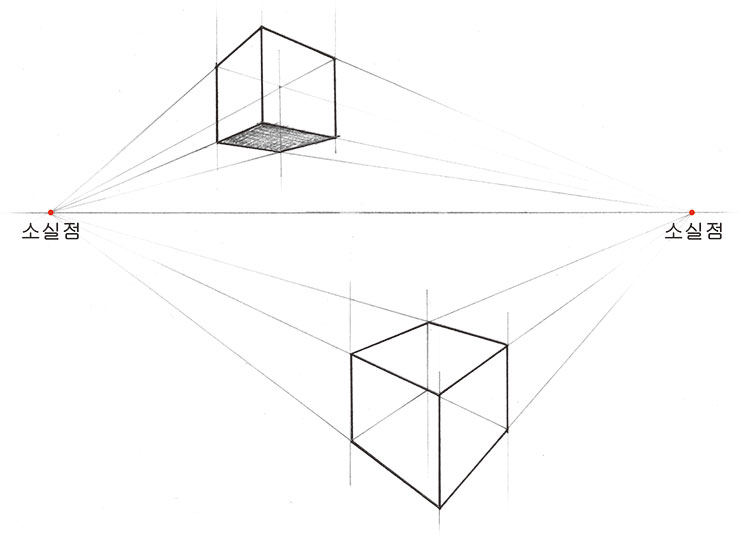
다음 포스팅에서 혼동하기 쉬운 2점 투시도법과 3점 투시도법을 비교해 보겠습니다.
구로구미술학원 / 전원미술학원 구로 캠퍼스